A Statistical Analysis of Climbing
February 17, 2014
Recently, 28 of us on the Stanford Climbing Team completed a short survey on our climbing abilities. Although the survey was intended to assess our interest in different clinics, the answers to the survey question also shed light on some interesting climbing questions, like how bouldering grades compare to top-rope grades, how much harder leading is than top-roping, and what different "climber types" there are. These questions really excited me, so I asked for permission to analyze this data, which the team graciously granted.
How Good are We?
The simplest question, though perhaps one of great interest to us on the climbing team, is simply how good the people on the team are at climbing, and how we compare to each other. Here's the distribution of how many of us climb at different levels:
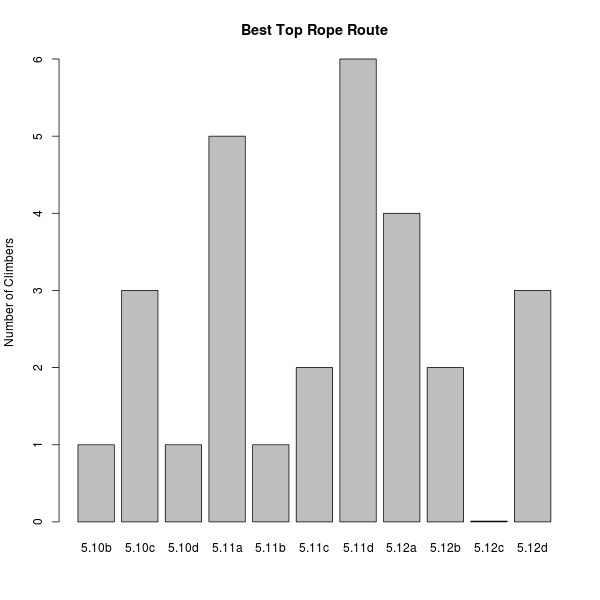
The average top-rope grade is slightly above 5.11c, with an SD of 2.8 quarter-grades. (I'm defining one quarter-grade to be the distance between a 5.10a and a 5.10b, or between a 5.11d and a 5.12a).
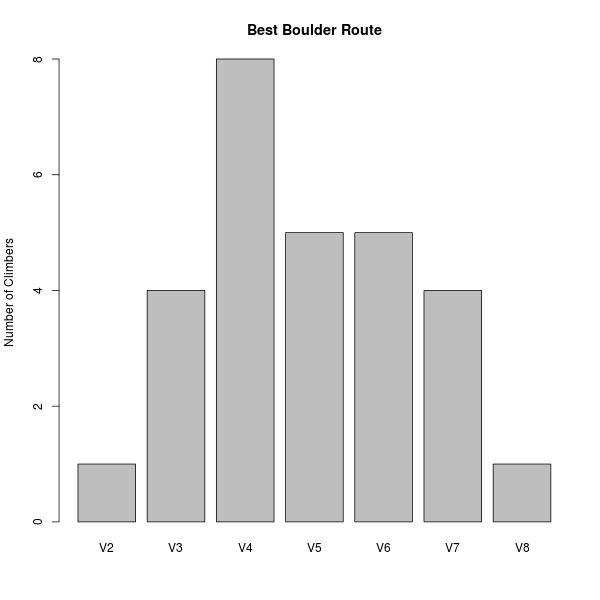
The average bouldering grade is slightly under V5, with an SD of 1.5 bouldering grades.
Bouldering vs. Top-Roping Ratings
A question of broader interest that we can answer with this data is about the relationship between ratings for top-rope routes and bouldering problems. What's the top-rope equivalent of a V4, or the bouldering equivalent of a 5.10c? To answer this, I plotted the best top-rope route people could climb against the best bouldering problem they could climb. There is a correlation of 0.89 between the ratings of the best bouldering and top-rope routes that people climbed, evidence that bouldering and climbing ability are strongly related, and suggesting that attempting to compare grades between them is reasonable.
There were several groups of people whose hardest bouldering route and top-rope climb were the same; these points, like (V4, 5.11c) are plotted darker in the below plot.
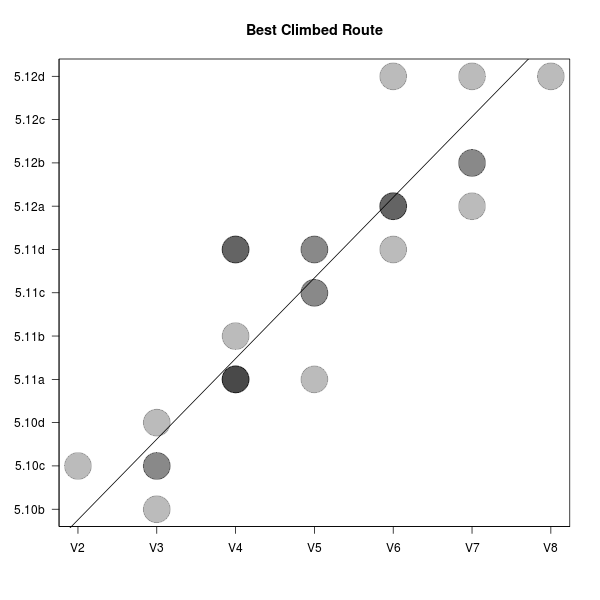
Because I wanted to establish an equivalence between the two difficulty systems, rather than asymmetrically predict one from the other, I used a total least squares linear regression (with standardization of the variables) rather than ordinary least squares. I've also plotted this equivalency line on the above plot.
I found that a difference of one bouldering grade is equivalent to about 1.9 quarter-grades for top-roping, (a 95% bootstrap confidence interval gives between 1.6 and 2.2 quarter-grades). I've listed the estimated equivalency in the below table. (Some bouldering ratings, like V4- and V4, are listed as having the same top-rope equivalency. This isn't because I estimate them to have the same difficulty, but rather because I rounded the estimated equivalent top-rope grade to the nearest quarter-grade).
| Bouldering | Top-Rope |
|---|---|
| V2- | 5.10a |
| V2 | 5.10b |
| V2+ | 5.10b |
| V3- | 5.10c |
| V3 | 5.10d |
| V3+ | 5.10d |
| V4- | 5.11a |
| V4 | 5.11a |
| V4+ | 5.11b |
| V5- | 5.11c |
| V5 | 5.11c |
| V5+ | 5.11d |
| V6- | 5.12a |
| V6 | 5.12a |
| V6+ | 5.12b |
| V7- | 5.12b |
| V7 | 5.12c |
| V7+ | 5.12d |
| V8- | 5.12d |
| V8 | 5.13a |
Extrapolating outside of this range would be questionable both because it would leave the domain that we have data on, and also because at the low range the scale changes. Is the difference between a 5.8 and a 5.9 equivalent to four quarter-grades, or something less?
Top-Roping vs. Leading Ability
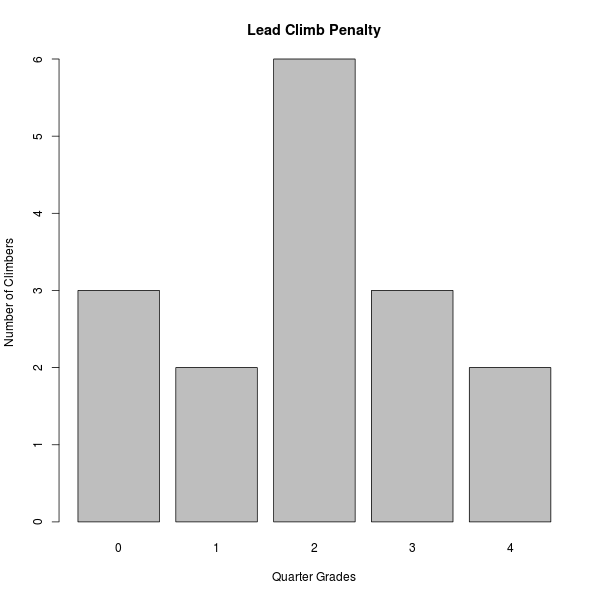
I think the majority of climbers would agree that lead-climbing is harder than top-roping. Personally, I climb about two quarter-grades softer on lead than I do on top-rope because of the much harder mental challenge that leading entails and because of the need to take a hand off the route to clip. Of the 28 respondents to the survey, 16 of us lead-climb. None of us lead-climbers climb harder on lead than they do on top-rope, but three of us don't suffer any performance penalty. Here's the plot of the leading performance penalty; we climb an average of 1.9 quarter-grades softer on lead than on top-rope.
Types of Climbers
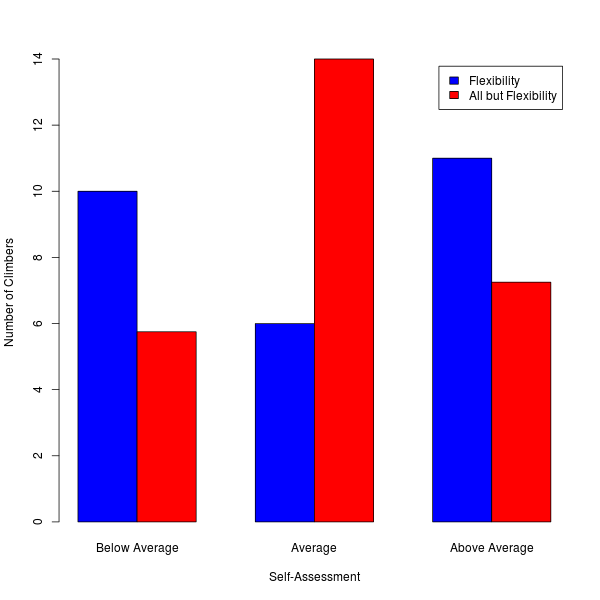
The survey also asked us to assess specific climbing abilities, like power, flexibility, endurance, and route-reading ability, relative to other climbers at our level. It gave us the options "Below Average", "Average", and "Above Average". This data is exciting because it gives us the ability to discover "types" of climbers.
Impressively, we seemed to be pretty even-handed in our self-assessments: Coding the abilities as 1, 2, and 3, none of the nine different climbing skills had an average that was statistically distinguishable from 2.0, and even after combining the resulting p-values with Fisher's method the differences remained statistically insignificant.
Amusingly, most everyone has a strong opinion of how flexible they are: Of the 27 people who answered the questions in the abilities section, only 6 said they had "Average" flexibility, compared to a mean of 14 climbers who said they were "Average" in each of the other eight skills.
To discover types of climbers, it's first very interesting to take a look at which abilities are correlated with each other. The chart below shows the nine skills that we were asked about, and the pairwise correlations between them. Blue-er ovals running from bottom-left to top-right represent higher positive correlations, while red-er ovals running from top-left to bottom-right represent higher negative correlations. Clear circles represent correlations near zero. The chart is symmetric about the diagonal because the correlation coefficient is symmetric in its arguments.
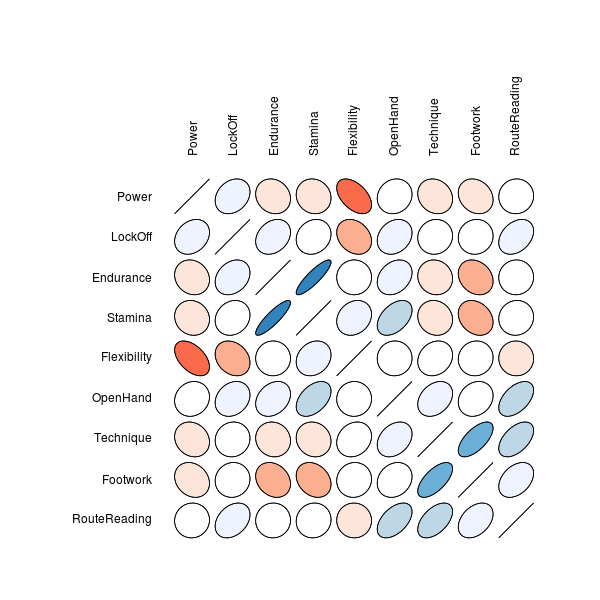
A few interesting relationships pop out from this chart: The most interesting one to me, (perhaps because it gives me an excuse to have difficulty reaching past my knees), is that more powerful climbers tend to be less flexible, and vice versa, (correlation -0.49). Also interesting to note is that the data clearly indicate the importance of footwork and route-reading in technique: The two are of course positively related with technique, (with correlations 0.65 and 0.51 respectively). The data also make clear that endurance and stamina are very closely related, (correlation 0.87). (Indeed, when I took the survey I tried to look up the difference on Wikipedia, but couldn't quite figure out what the difference was after a quick skim).
To distinguish types of climbers, I tried both k-means and a principle components analysis. Both the cluster centroids from k-means and the PCA essentially said that there are two main axis that most distinguish types of climbers: The flexibility-power spectrum, and the spectrum between having and not having climbing-specific skills like good technique, good open-hand strength, and good footwork. The following biplot shows the results from the principle components analysis, the first two components of which capture 51% of the variation in climbing skill. On it you can clearly see the power-flexibility and the climbing skills spectra.
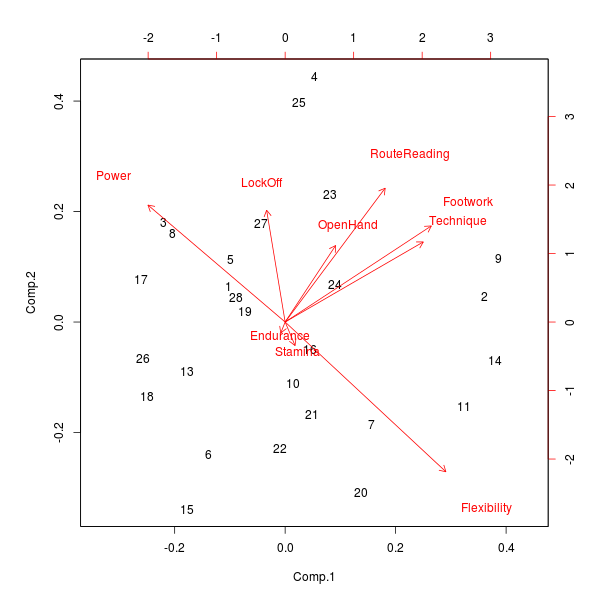
Unfortunately, one of the variables the data are missing, gender, is potentially a major confounder that could mess up some of these interpretations: The survey did not ask for our gender, which unfortunately could be at the root of some of these correlations, especially the relationship between power and flexibility. It's reasonable to suspect that men are more powerful and less flexible climbers than women, resulting in the relationship we see, but that among men and among women there is no relationship between power and flexibility.

