Don't Double Major
April 8, 2014
Double majoring in college is a very suboptimal strategy. The reason is simple: It adds a substantial set of constraints to the courses you can take, but in return gives you only a very modest extra credential.
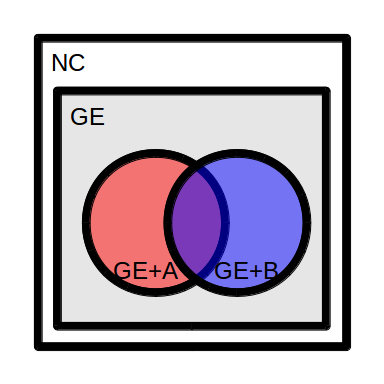
In the above diagram NC ("no constraints") is the set of all possible course schedules you could take during college, like "Freshman fall: Math 101, Econ 101, Chem 101, Hist 101; Freshman Spring: Math 102, Econ 102, Chem 103, Art 102...". For each possible course schedule, there is some utility that you would derive from it if you were to take those classes in that order. This utility is some combination of what you would learn, how much you would enjoy yourself while doing so, how you would develop as a person, and so on. If there were no constraints on the courses you would take, you would presumably choose the schedule that maximized this utility to you.
In the diagram GE ("general education") is the set of all schedules that also satisfy the general education requirements. GE might, for example, include only the schedules that include two classes each from the humanities, social sciences, and natural sciences. Finally GE+A and GE+B are the set of schedules that also satisfy the major requirements for major A or major B, respectively. Let's call their intersection GE+A+B, the set of course schedules fulfilling the GE requirements and the requirements for both majors.
My central point is that as you add more and more constraints, the set of schedules you can take shrinks, and the maximum utility you can achieve from the fewer permissible schedules therefore decreases as well. Mathematically, this is simply the fact that the maximum of a subset is no larger than the maximum of the superset. Now, I've put this in mathematical terms, but even an English major who suffered through a required pre-calculus class can relate to the fact that they would have achieved a higher utility by replacing it with a Shakespeare seminar.
In particular, my argument that you shouldn't double major boils down to the fact that the highest utility you can get from GE+A+B is in general lower than the highest utility you could get from the union of GE+A and GE+B. For example, the fact that you have to fulfill both sets of requirements to double major in Math and CS means that you need to take Abstract Algebra or Computation Theory when you might really be a lot more interested in computational math. In this case, instead of double majoring, you should take all the computational math classes and anything else that interests you, and then major in math or CS depending on which one is easier to get. This way, you won't have to take both Algebra and Computation Theory, just one of them, and can replace the other with something that's more interesting to you.
Note that my argument to avoid double majoring is not an argument in favor of specializing over generalizing. Many times, in fact, quite the opposite is true: Though I majored in Statistics in college, I also took classes in Chemistry, Math, Computer Science, and, (no surprise), Economics. Had I added a double major in one of these disciplines, I would not have had the free space in my schedule to study all of the other disciplines that I did. Had I double majored in Chemistry, for example, I would have had to take Organic Chemistry, which might have meant that I wouldn't have had time to study Industrial Organization or Computer Architecture. Not only would this have been a substantial loss for me, (since I'm a lot more interested in IO and Architecture than I am in O-Chem), but I'd also be less of a generalist than I am today.
What do you gain from double majoring then? As far as I can tell, all you gain from a double major is an extra line on your diploma and resume--it gives you slightly improved credentials. Even that is frankly dubious, as there's nothing stopping you from adding a line with "relevant coursework" on your resume. And whatever value the credential does have will presumably shrink after a few years of work experience or after earning an advanced degree. In short, it's clearly not worth it.

