Map Transformation

March 23, 2018

Note: I was describing my map transformation project to Sasha Trubetskoy recently, who is even more into maps than I am. This is a project I completed in March 2011 with Shir Yehoshua for a CS class, where we transformed a map of Washington DC so that the Euclidean distances on the transformed map became more proportional to travel times. I've described this project many times over the years to various friends, and figured that it was long past time I wrote it up. What follows is a write-up that's partly based on contemporaneous emails I wrote about this project, and partly based on my now-hazy recollection:

I conceived the idea for this project during the summer of 2010 in Peru, while my travel partner and I were on a bus on a rocky, windy, dirt road somewhere in the very rural part of the country. It was an ongoing joke between us that all the budgeting of our time we had done before the trip was worthless, since some things took much longer or shorter than our estimates. In the most egregious case, I thought that since the city of Chachapoyas was only something like 50 km both from a waterfall and from a large fortress, we could see one in the morning, the other in the afternoon, and then check out part of the city in the evening. In fact, it turned out that because of the terrible road quality and the only sporadic availability of transport, the falls alone took an entire day and the fortress was an overnighter.

This got me thinking that the maps we were relying upon had been in a certain sense misleading. For human beings, two locations are far away from each other not if they are separated by many miles, but rather if it takes many hours to travel between them. Physical maps can misrepresent geography because some locations appear close but are in fact far, and some locations appear far but are in fact close. On that bus I had this idea: What if you could take a map and transform it so that the distances on the transformed map were aligned more closely with travel times? This transformed map would then be a more honest representation of the geography for human purposes.

We ended up choosing to transform a map of the Washington DC area instead of Peru or some other place because most of the area on an image of Washington is accessible by car, (unlike, Peru, which has a lot of jungles, mountains, and rural areas, or a coastal city, with the ocean nearby). The reason it's hard to use a coastal city or an area with a lot of wilderness is that the time distance between two points, if one of them is in the wilderness or water, is huge, (you'd have to walk or swim). As a result, on the transformed map any wilderness or water areas should "blow up" to represent the large time-distance to and within them. This would make the resulting map uninformative (and look dumb).

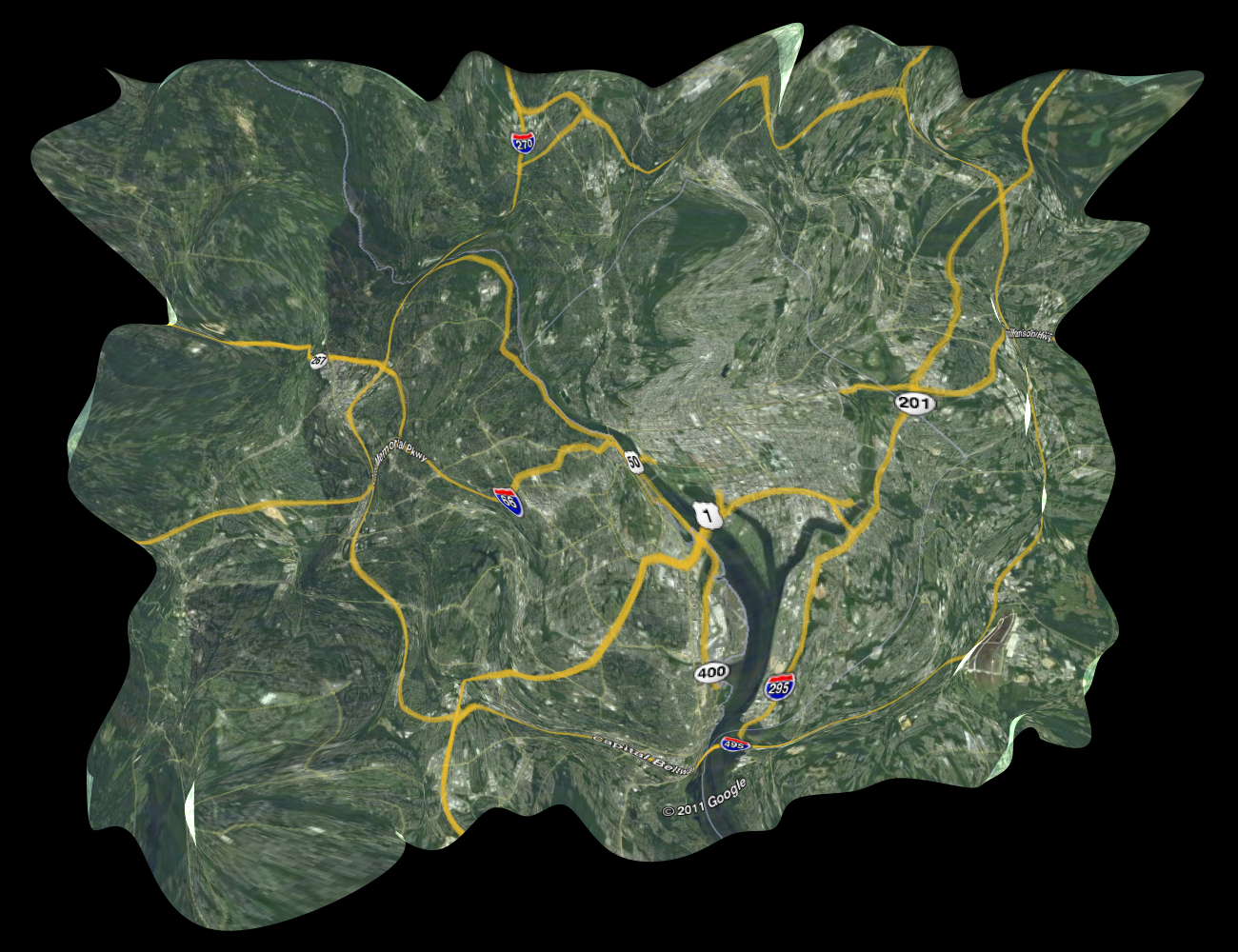
Here are the final "before" and "after" pictures; the rest of the post goes into details of how we implemented this.

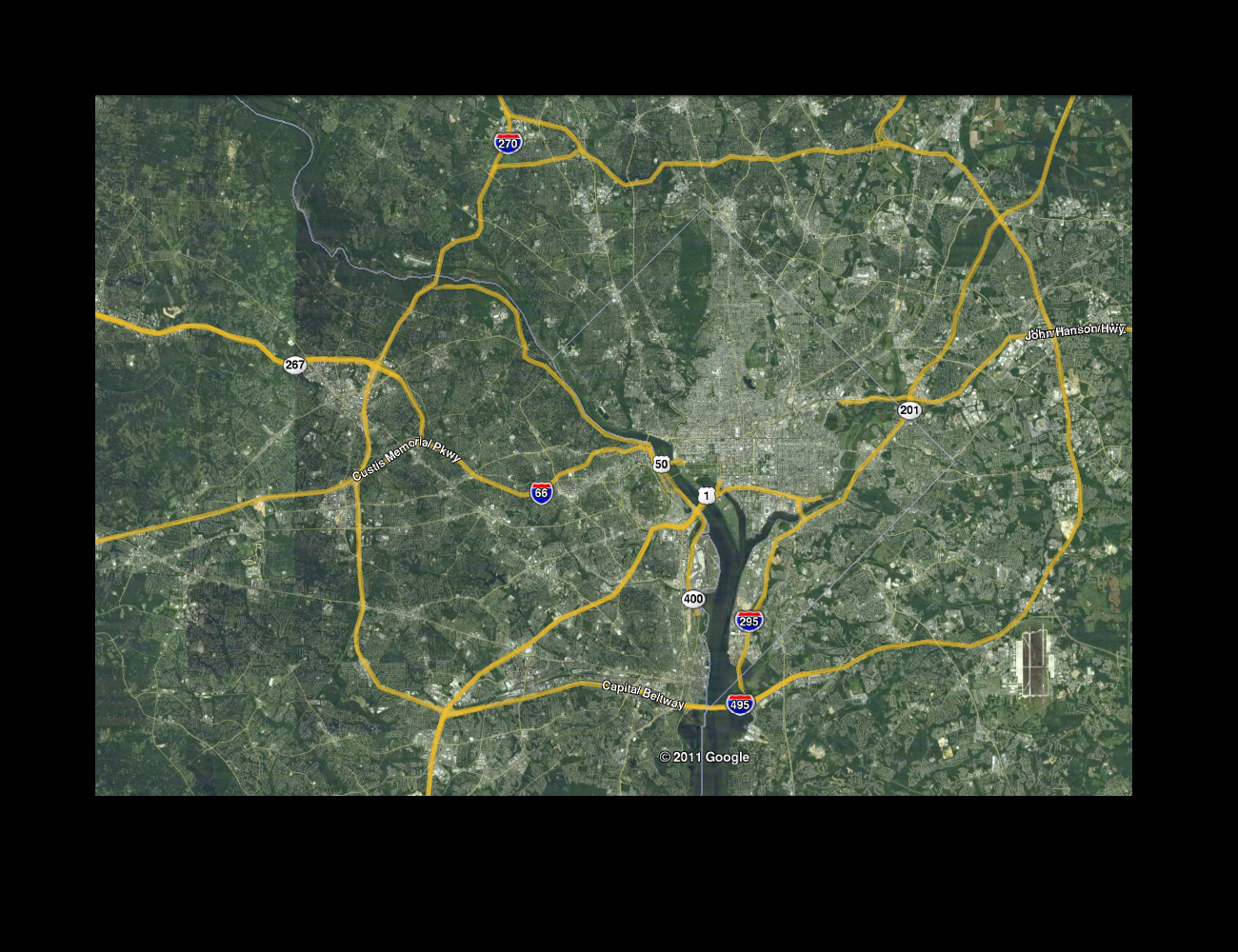
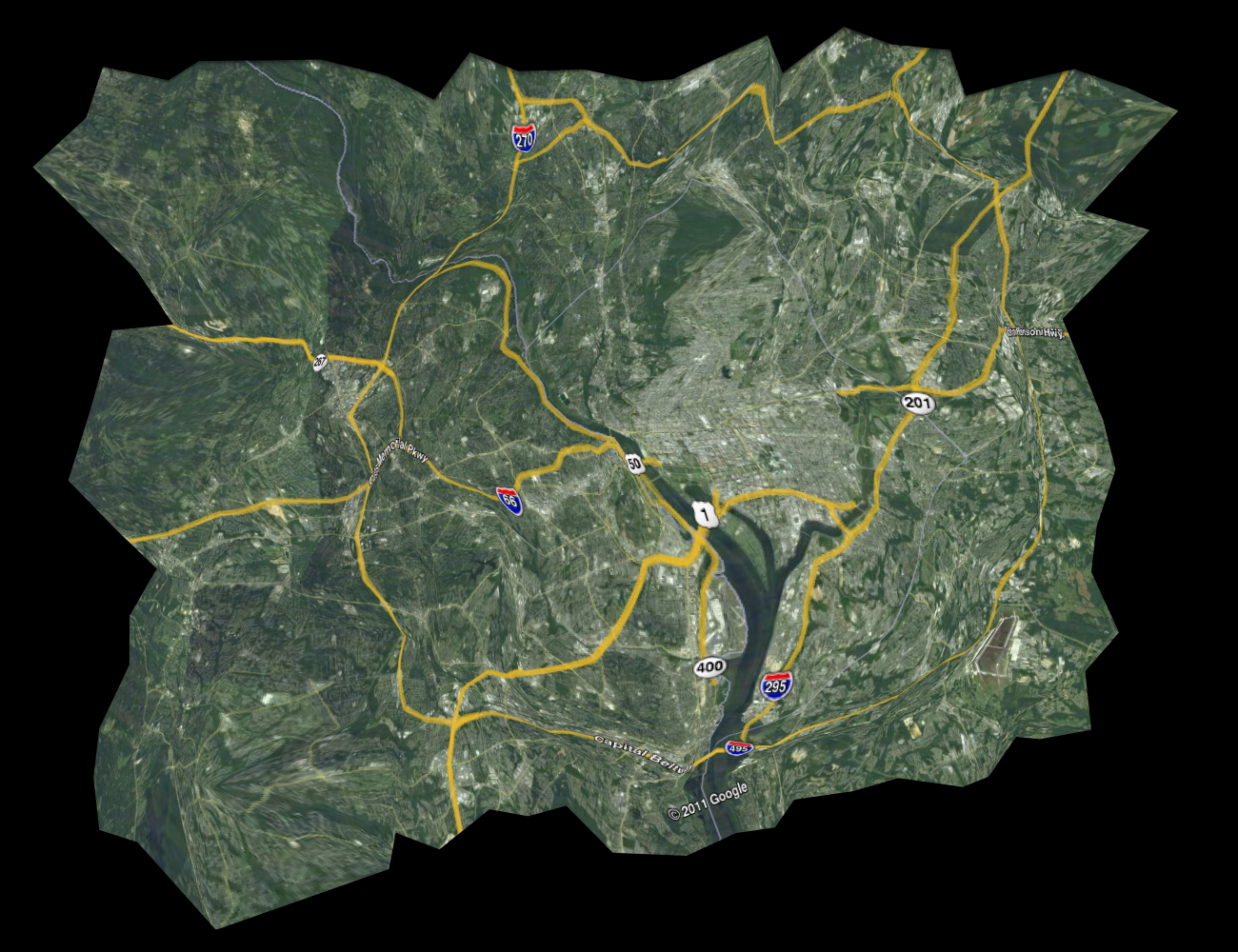
Some of the more intuitive features of this transformation are that the two east-west freeways on the west part of the map contract, the beltway scrunches up, and the Potomac river expands.

This project had four main parts:

1. Getting travel times between the grid-points on a map
2. Computing the transformed location of those grid-points
3. Extrapolating the transformation from those grid-points to arbitrary (x, y) coordinates
4. Taking the resulting transformation function and applying it to an actual map image

Getting travel distances between grid-points

First, we needed to collect a lot of data on travel times. We did so by writing a script to get travel time estimates from Google maps. We obviously couldn't get the travel time from every location on a map of DC to every other, so we overlaid a 21 x 14 rectangular grid on top of Washington and only queried the travel times between grid points. We didn't assume that the travel time from A to B was the same as from B to A, so in the end we had to make some 86,142 queries.

I don't have any documentation or code on how we did this, but I recall it actually being fairly hard. At the time the free API limited you to 2500 queries a day. I believe we screen-scraped with Selenium, possibly across a number of CS machines. (Sorry, Google...!)

Computing the transformation of the grid-point

Once we had the travel times data, we needed to figure out how to transform the map. Ideally, the distances on the transformed map would in fact be directly proportional to the travel times, but this is clearly impossible in general, even ignoring the fact that travel times vary by time of day and have random components. Because of this impossibility, we instead had to find the "optimal" transformation, and came up with a number of possible objective functions to minimize. The following plots show how the grid-points were transformed under various different objective functions:

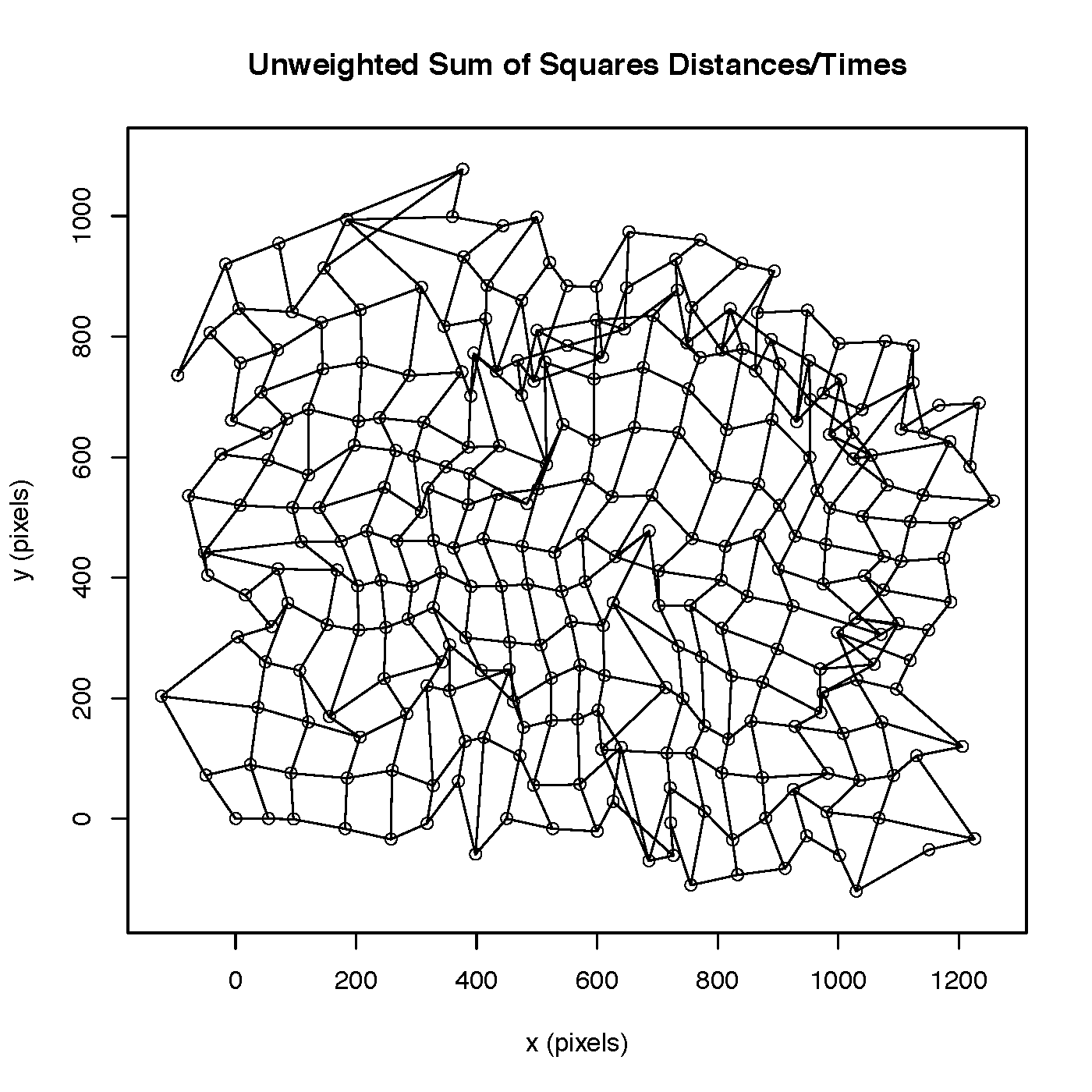
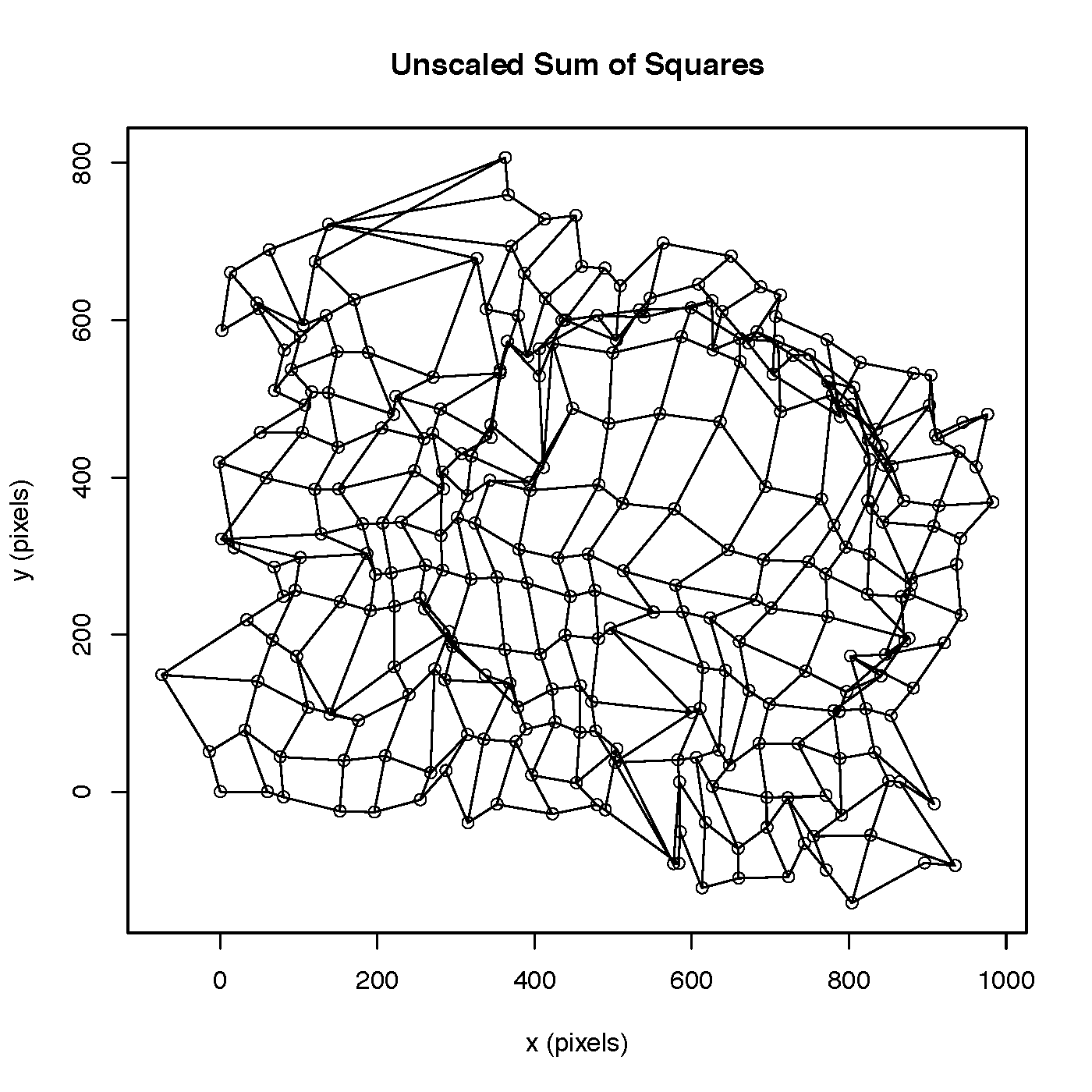
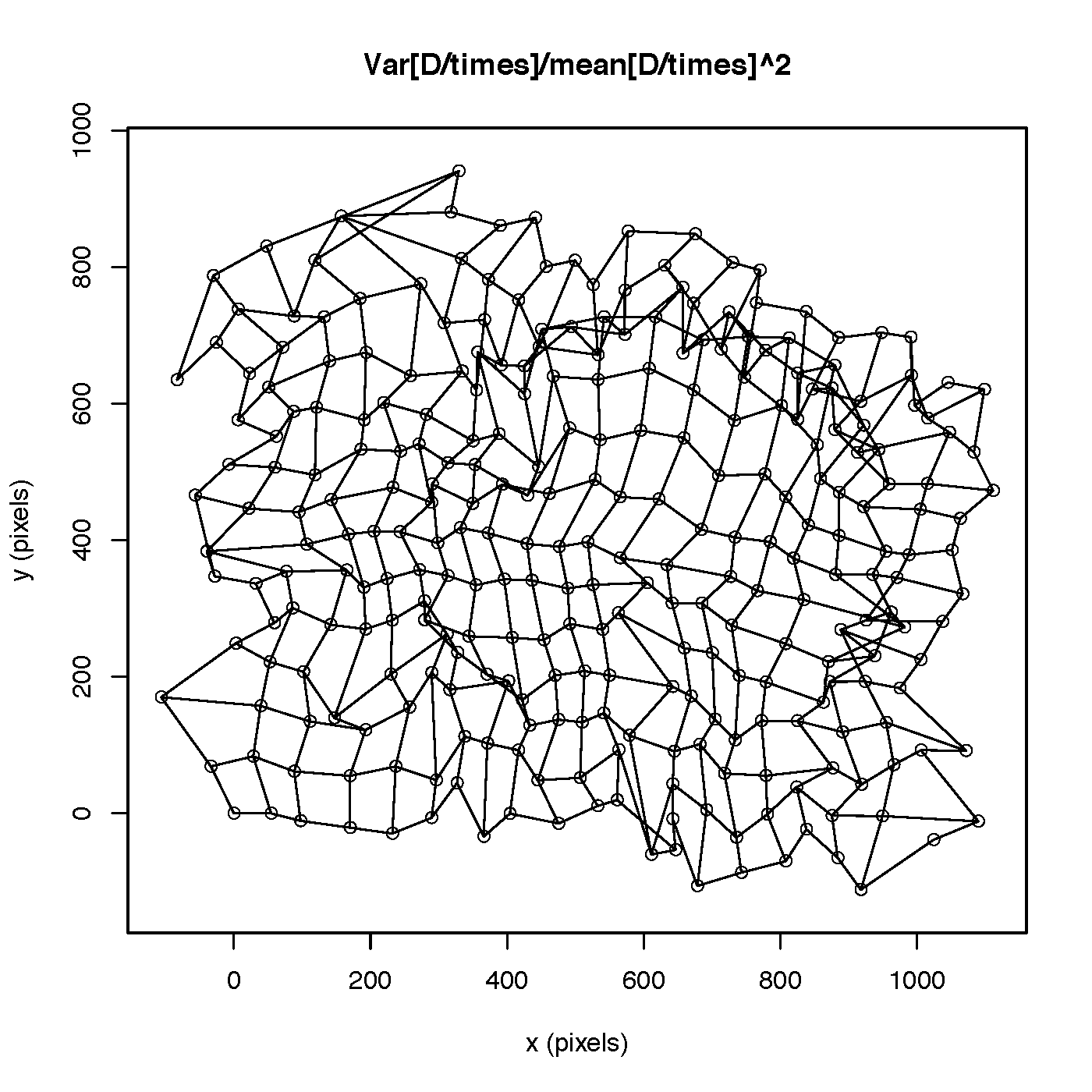
The one we ended up using we called "negative cosine minimization." We treated the matrix of travel times and the matrix of distances on the distorted map as vectors, and chose the new locations of the grid-points to minimize the angle between these matrices. More precisely, if T is the matrix of travel times and D is the matrix of distances between grid points on the transformed map, we chose the 294 new locations of the grid-points, (588 parameters), to minimize: - tr(T' * D) / sqrt( tr(T' * T) * tr(D' * D) ). This produced the following transformation of grid points:

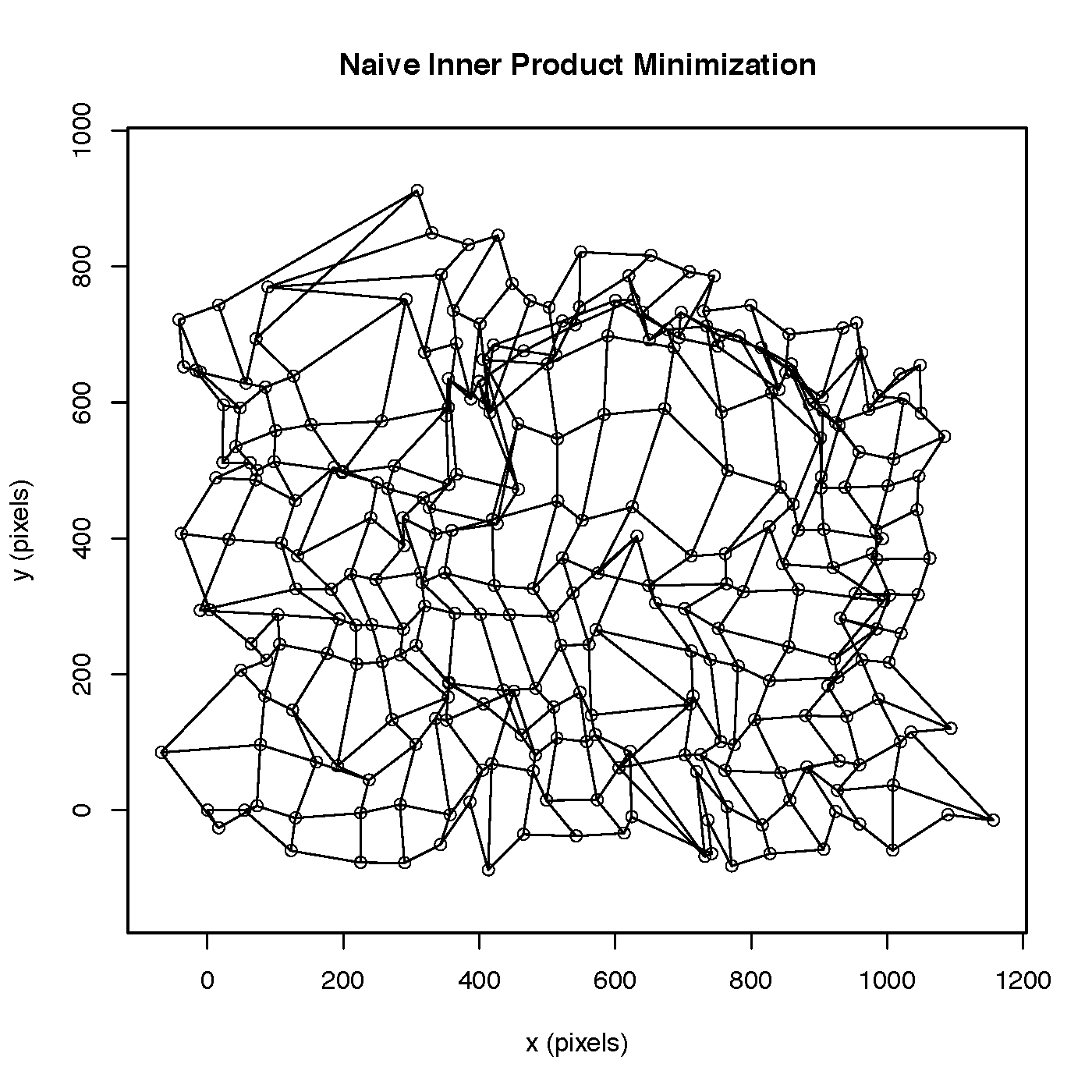
Unfortunately, solving this optimization problem without any constraints on the new locations of the grid-points yielded ugly transformations, with folding over of grid lines that is hard to interpret. (You can see this particularly in the top beltway region in the above transformation, as well as some in the left part of the beltway and the top-left corner of the map).

To avoid this issue, we added the constraints that the rectangles on the initial grid needed to transform to convex quadrilaterals. (I honestly don't recall why this implies that the grid-points can't fold over, but apparently it does as you can see from the next plot). This turned out to yield 1040 quadratic constraints. We then solved this problem with the SQP algorithm to get the following transformation of grid points:

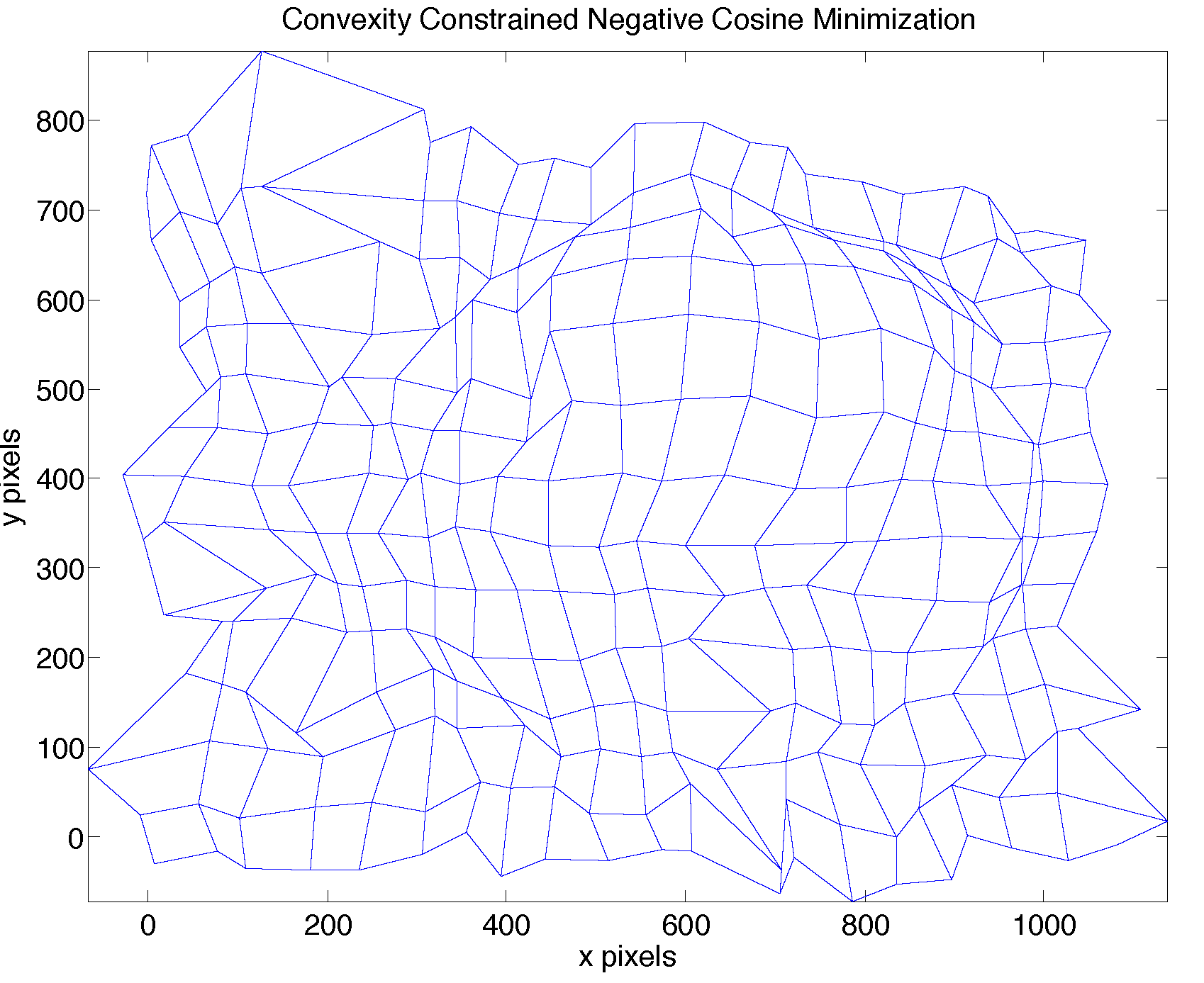
Extrapolating the transformation

We then tried to extrapolate a nice continuous transformation from the new locations of the 294 grid-points. Ideally, wanted to find a continuous transformation that:

1. transforms the grid-points to their new locations
2. has a continuous Jacobian
3. does not "fold over" (ie, is injective)

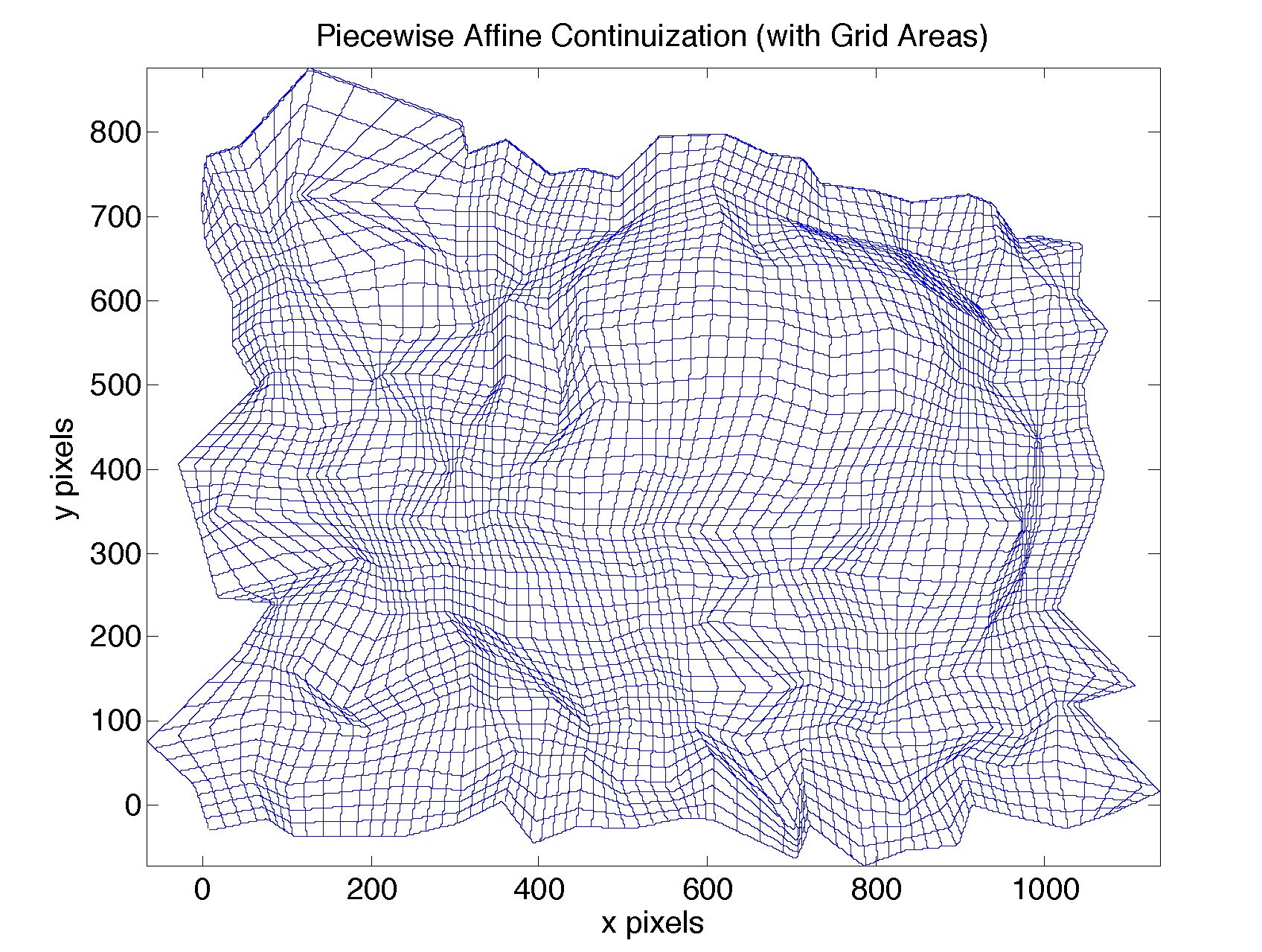
Extrapolating to a piecewise affine transformation did not have a continuous Jacobian and thus looks a bit "patchy".

Unfortunately, extrapolating with cubic spline polynomials led to some "folding over", where multiple points on the original map were transformed to the same point on the resulting map:

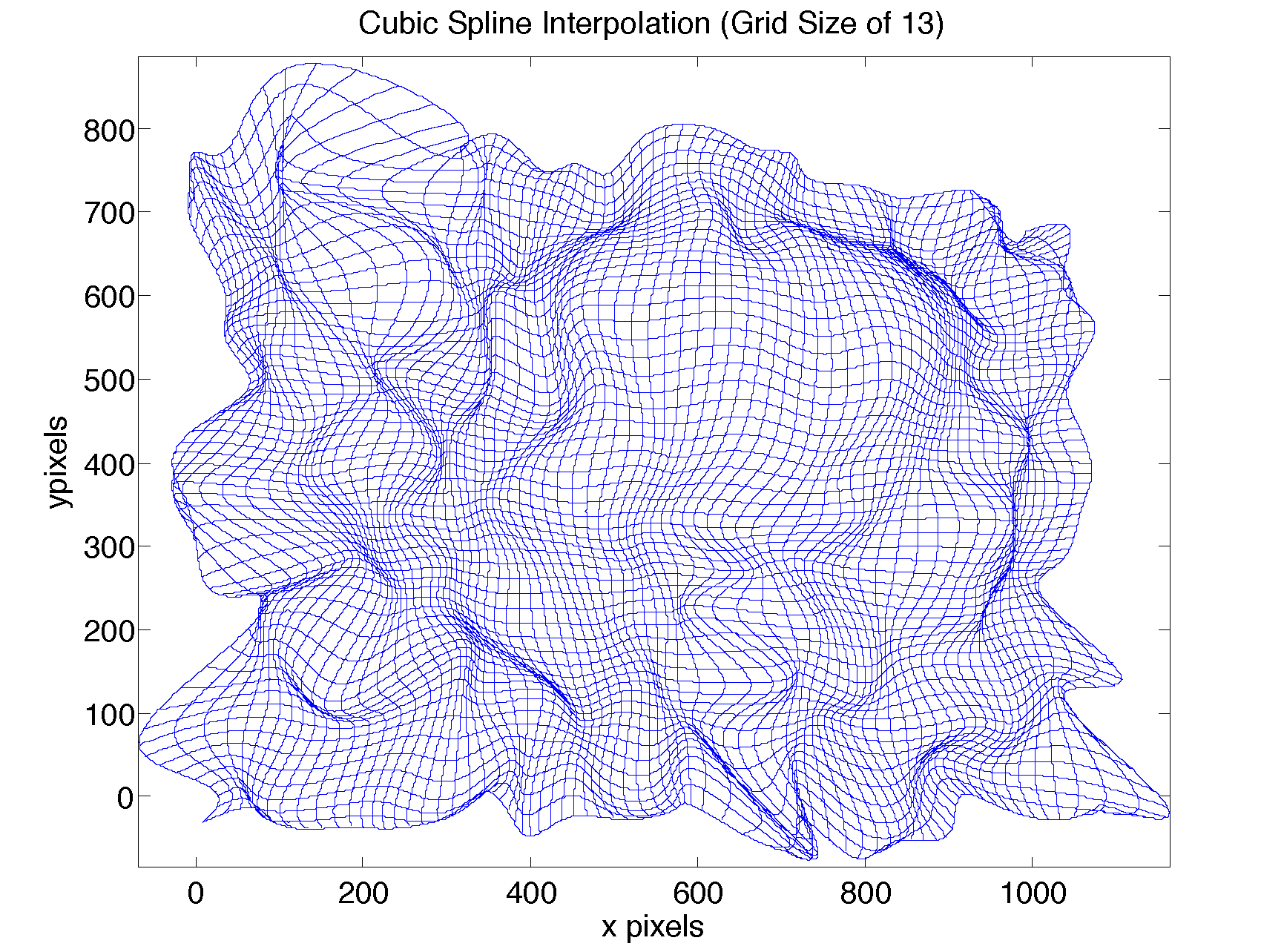
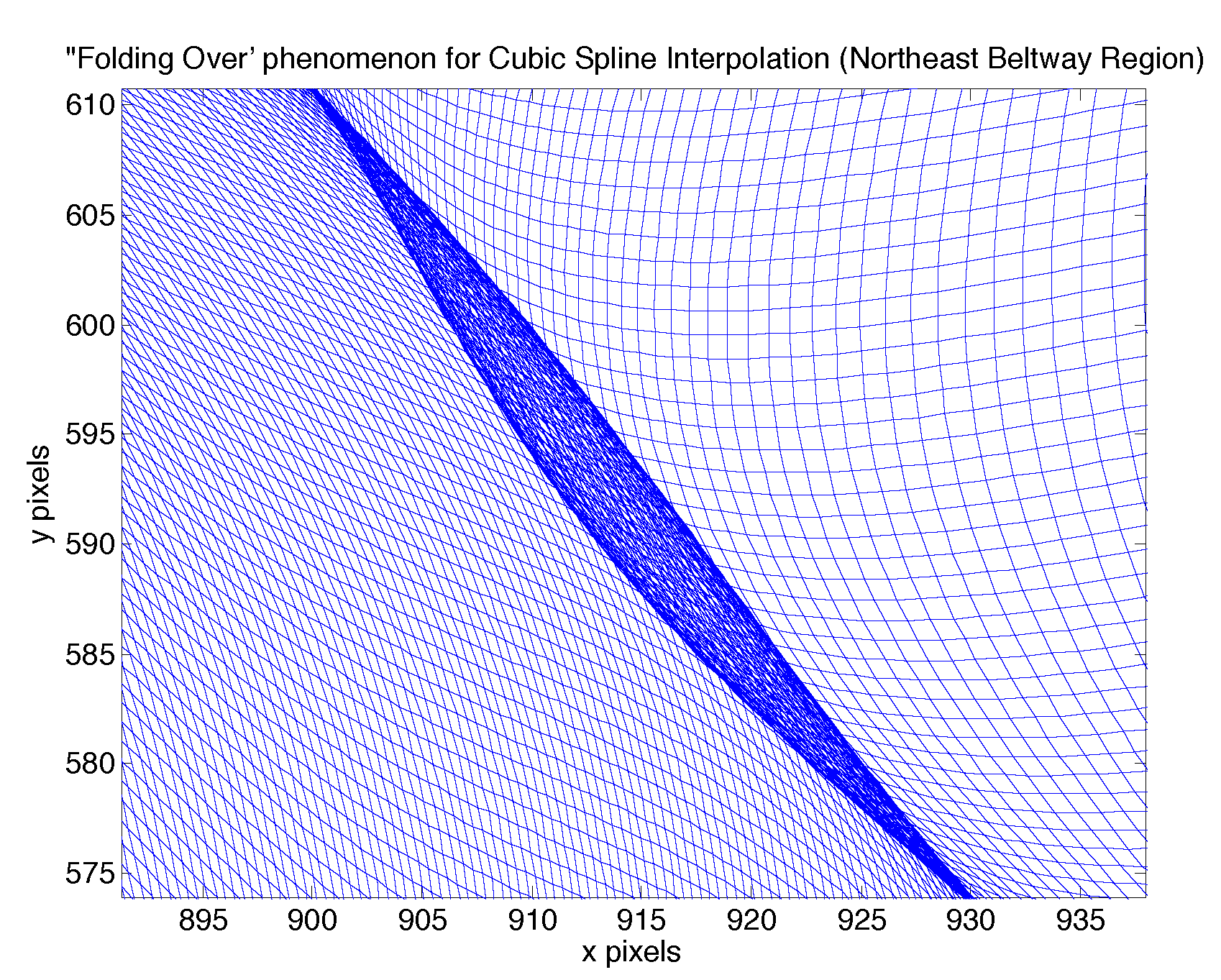
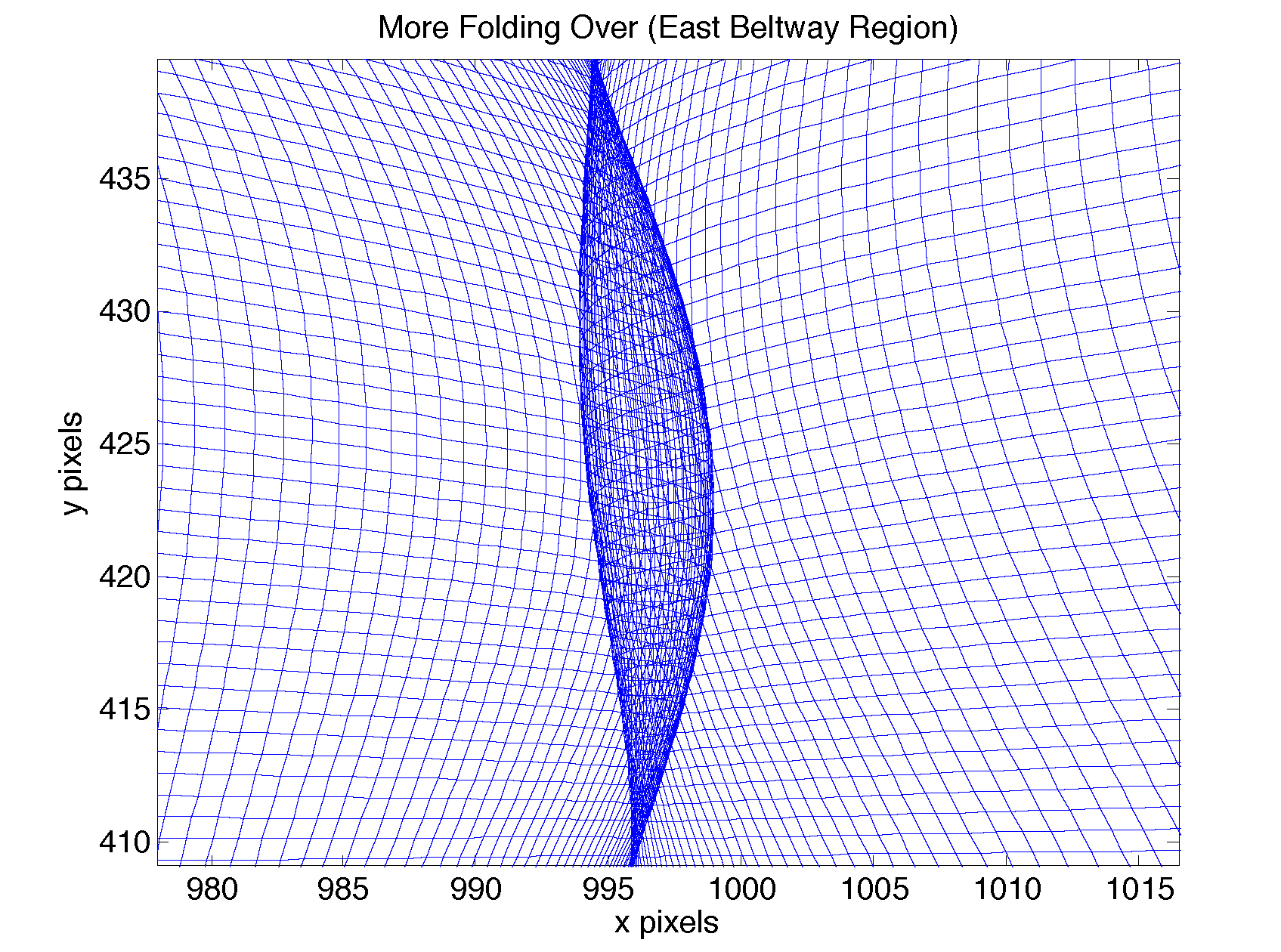
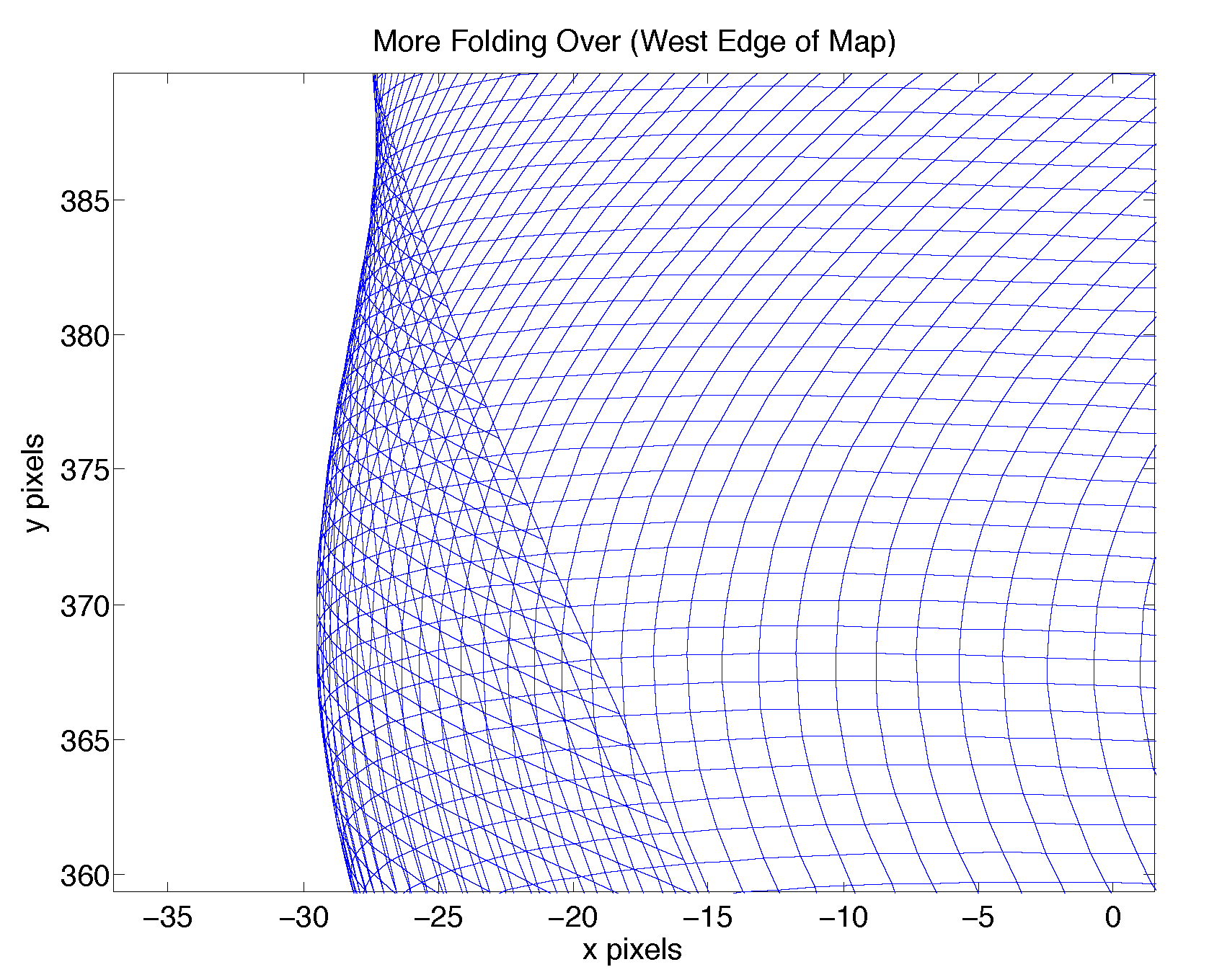
We decided that "patchiness" is better than folding over, so picked the piecewise-affine extrapolation rather than the cubic-spline extrapolation.

Applying the transformation to the map image

Unfortunately the contemporaneous write-up I have in my email doesn't go into much detail here. I remember this being pretty interesting as well, though--we couldn't find a library to do this and actually wrote pixel-level code instead. Much geometry was involved! For the piecewise affine extrapolation and the cubic spline extrapolation, this produced the following images:

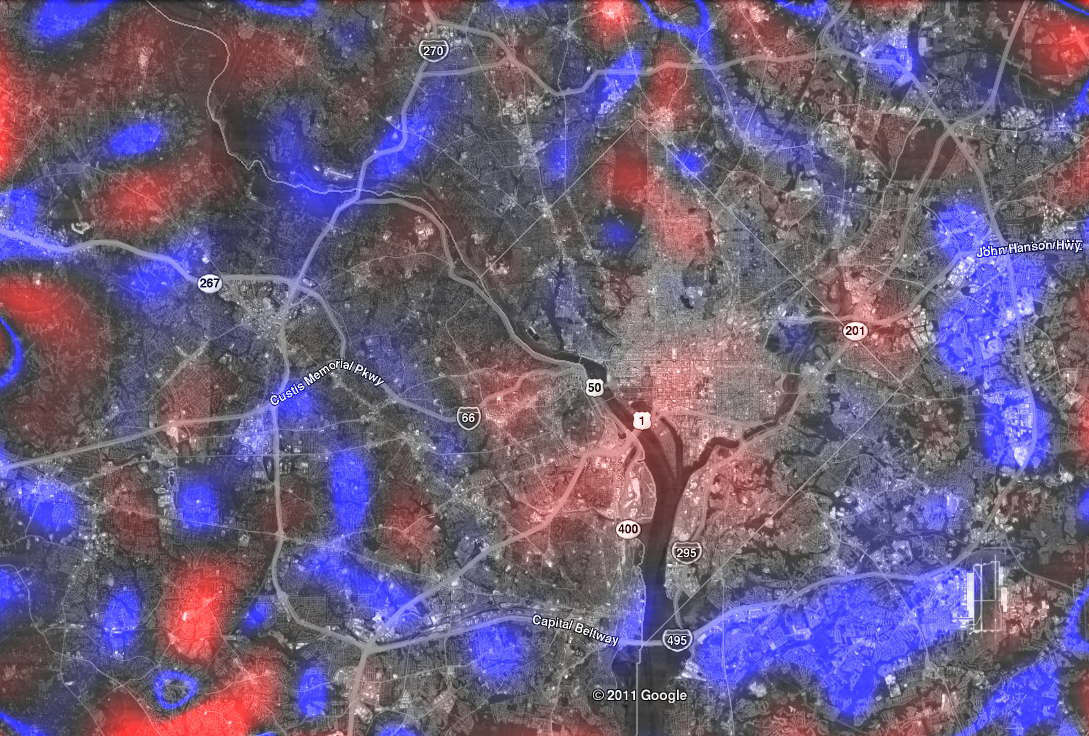
For both of these transformations, we also plotted the determinant of the Jacobian on the original map, which describes how much an area is growing or shrinking in the transformation. In the below, blue areas are those that shrink, and red areas are those that grow:

You might also enjoy...

• Day-to-Day Operations of Palo Alto
• OHMS Lessons Learned
• Visualizing K-Means Clustering