Memory Locality and Python Objects
April 15, 2013
I've been obsessed with sorting over the last few weeks as I write a python C-extension implementing a lazily-sorted list. Among the many algorithms that this lazily-sorted list implements is quickselect, which finds the kth smallest element in a list in expected linear time. To examine the performance of this implementation, I decided to plot the time it takes to compute the median of a random list divided by the length of the list. Theoretically, since quickselect runs in expected linear time, this plot should be roughly constant. In fact, this is what the plot looks like:
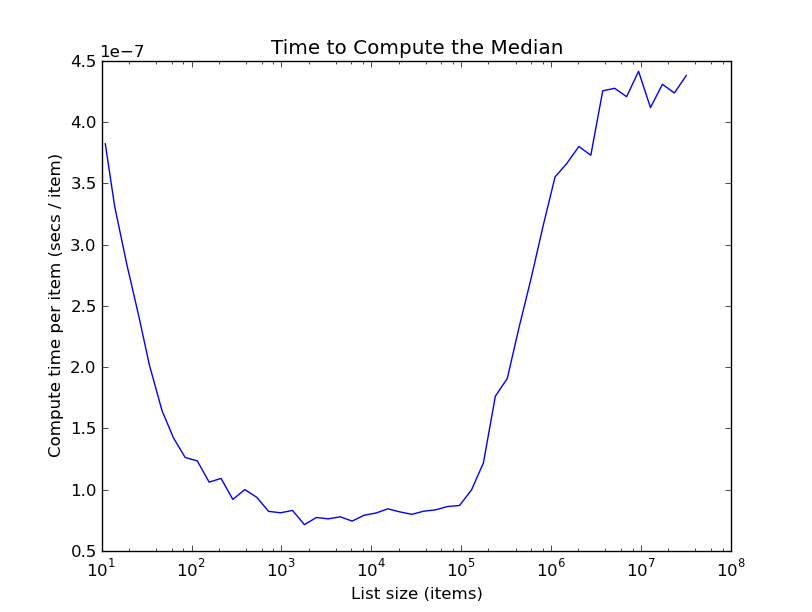
The first part of the plot is understandable: the time per item drops quickly with list size as startup costs get amortized over more data. But the truly bizarre thing is that after lists get bigger than about 100K, the time per item starts to increase massively! What's going on? In the rest of this post I describe the things I tried to find out:
Reviewing the code
At first I thought there might be some simple mistake in my implementation. I was quite confident that my implementation actually produces the true median, because I have pretty extensive testing code, but I worried that perhaps it was doing some excess computations mistakenly. So I carefully reviewed my code a few times and couldn't find anything wrong. Not immediately finding anything wrong isn't conclusive, of course, so I kept looking.
Profiling the program
Unlike the usual quickselect, I also keep state about where the pivots are, and accumulate overhead from interfacing with python. I therefore worried that this overhead might be the source of the increased time. But profiling indicated that the program spent almost all its time doing partitions, which it's supposed to. Since this was my first time profiling a python C-extension, to be extra-sure I quickly commented out the lines keeping track of pivots, but the large-n cliff phenomenon remained.
Watching the program in gdb
To gain more insight about what was actually going on, I watched a large list get sorted in gdb. This was valuable; it showed that many of the early partitions were very wasteful, since the pivot point ended up being near the front or back of the list. So I changed my pivot selection procedure from picking a point uniformly at random to picking the median of three random points. This increased the overall speed by around 30%, but didn't get rid of the large-n cliff phenomenon. Watching a large list get sorted in gdb also showed me that my algorithm was doing what I thought it was doing; it was implementing quickselect as I understood it.
Simulating the algorithm
Now I have a general mistrust of asymptotics, and so I was somewhat worried that the time complexity theory did not align well with practice. Although I thought it was something of a longshot, I decided to test this by writing a throwaway quickselect simulator in R. This indicated, that, as claimed by the theory, quickselect does indeed run in linear time for finite n.
Writing a Simpler Version
At this point, I was pretty frustrated, having been debugging for several hours and still without a clue of what was causing this behavior. My best remaining idea was that out of all the things I'd tried, the least effective was the one where I just reviewed my code for bugs. So I figured that if I independently wrote a new, simplified version of quickselect to just select elements from arrays in C, without referencing my previous code, then maybe I would realize my mistake. Moreover, if the simplified quickselect ran in linear time, I'd be able to compare it to my more complicated implementation for python, and if it had the cliff phenomenon, then I'd at least have an simpler program to analyze for bugs.
So I wrote a simple program in C, about 100 lines, (compared to 1000+ total for the complicated C-extension), to select the kth smallest element from an array of int's. And it ran in almost exactly linear time; running it on lists 10 times longer basically just moved the decimal point on the timing. So I compared the simple program to the complicated C-extension, but both implementations used the same algorithm and no bugs were uncovered.
Figuring it out
Finally, I had the epiphany that solved my problem: Since objects in CPython are passed around as (PyObject *)'s, that is, pointers to some data, you run into the following memory access problem: Quickselect itself is reasonably good at preserving data locality, so when you have an array of int's, quickselect runs nice and fast. (Partitioning, the bottleneck of quickselect, keeps track of two locations--the index of the element being examined in the list and the last index that's less than the pivot. These both change slowly as you iterate through elements in the list). But when you shuffle an array of pointers to data, then the pointers will all point to arbitrary places in main memory, so every time you dereference one of these pointers, it will lookup some random place in main memory. When the list isn't that big, this isn't a big deal--it fits in your cache. But as the list size grows, those random lookups lead to continual cache misses, and hence slow code.
Validating my theory
Thus, I figured, it would actually be more realistic for my simplified quickselect program to sort an array of pointers to int's, rather than the int's themselves. So I made this change, and, finally, reproduced the large-n cliff! You can try it too--here's the code! The plot for sorting the (int *)'s looks like this:
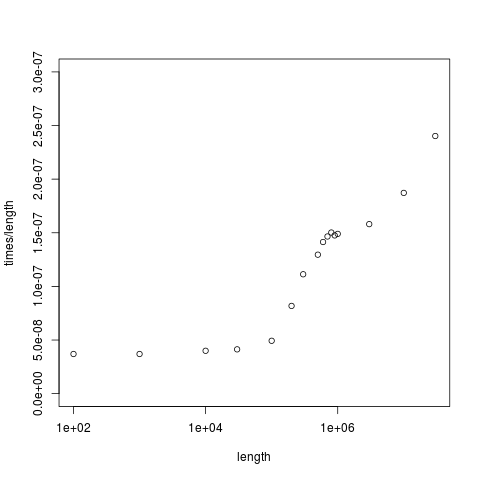
Some further evidence that cache misses are the source of large-n cliff comes from running the two quickselects on int's and (int *)'s through cachegrind, and observing the higher rate of cache misses. Also, on the machine that I ran this code on, my largest cache is 3MB, with a line size of 64 bytes, giving me 50K cache blocks. Now my simplified code starts hitting the cliff for lists of size about 100K, which is of the same order as the number of cache blocks. This ballpark figuring, I think, provides some further corroborating evidence for my theory.
Conclusion
Discovering the source of this behavior is in some ways pretty disappointing, because as far as I can tell there is nothing I can do to fix it short of a massive rewrite. I imagine that I could reduce the scope of my code without too much difficulty to operate on numpy arrays, which are implemented as arrays of values in memory, but that would lose the nice imitation of the sorted builtin, making my code substantially less generally applicable. The only consolation is that this poor behavior at scale is not my fault, but rather is due to fundamental implementation decisions in CPython. This is part of the performance price we pay for the convenience of coding in python.
EDIT: In turns out that you actually can solve this problem, using the __builtin_prefetch function in GCC and Clang. See my post about how I added a single line of code and got a 2x speedup for the details.

