Visualizing the James-Stein Estimator
May 6, 2013
In the words of one of my professors, "Stein's Paradox may very well be the most significant result in Mathematical Statistics since World War II." The problem is this: You observe $X_1, \ldots, X_n \sim \mathcal{N}_p(\mu, \sigma^2 I_p)$, with $\sigma^2$ known, and wish to estimate the mean vector $\mu \in \mathbb{R}^p$. The obvious thing to do, of course, is to use the sample mean $\bar{X}_n = \frac{1}{n} \sum_{i=1}^n X_i$ as an estimator of $\mu$. Stein's Paradox is the counterintuitive fact that in dimension $p \ge 3$, this estimator is inadmissible under squared error loss.
More precisely, we take the loss incurred when estimating the mean $\mu$ as $\hat{\mu}$ to be $\|\mu - \hat{\mu}\|_{2}^2$, the squared Euclidean distance between $\mu$ and $\hat{\mu}$. We can then measure the (lack of) quality of an estimator by its risk function $R(\mu) = E_{\mu} \|\mu - \hat{\mu}\|_{2}^2$, which is the expected loss when the true mean is $\mu$. It's easy to show that the risk of the sample mean $\bar{X}_n$ is a constant $p \sigma^2 / n$ for all $\mu$. The James-Stein Phenomenon is that that there exists an estimator $\hat{\mu}$ that has risk $R(\mu) < p \sigma^2 / n$ for all $\mu$. In particular, Willard James and Charles Stein proved in 1961 that the estimator $$\hat{\mu}\left(X_1, \ldots, X_n\right) = \left(1 - \frac{(p -2) \sigma^2 / n}{\|\bar{X}_n\|^2}\right)\bar{X}_n$$ has this property, and is therefore a strictly better estimator than the sample mean $\bar{X}_n$. This estimator is known as the James-Stein estimator.
As you can see, the James-Stein estimate $\hat{\mu}$ is just the sample mean shrunk towards zero. A good intuitive reason I've heard for why this might be better than the sample mean is that a good estimator of $\mu$ should spend most of its time being about distance $\|\mu\|_{2}$ away from the origin, or distance squared $\|\mu\|_{2}^2$ from the origin, while the expected squared distance between the sample mean and the origin is actually $\|\mu\|_{2}^2 + p \sigma^2 / n$, that is, too far away from the origin on average. The standard proof for why the risk of the James-Stein estimator is less than the risk of the sample mean, however, is based on a long computation, and I don't really feel it captures the key insights about what's really going on. Despite the exact finite-sample theory, this makes it hard to really believe that this phenomenon is not just a mathematical curiosity, like the one-dimensional shrunken mean estimate that I considered a few months ago. So I decided to visualize the James-Stein estimator to see how it really behaves.
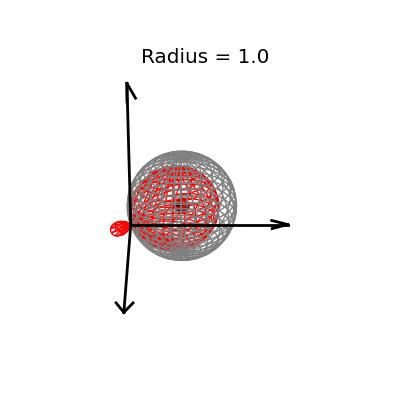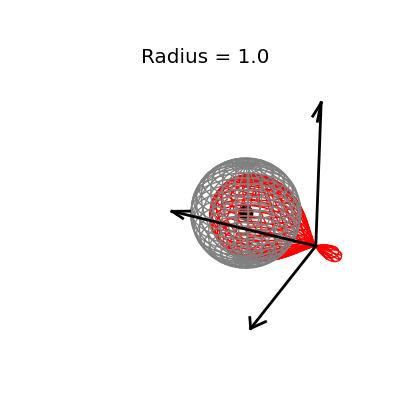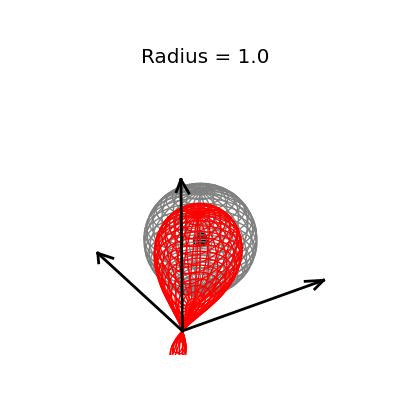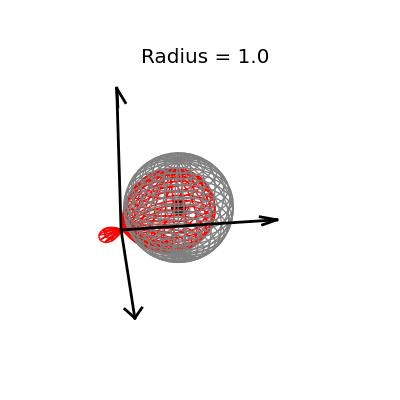
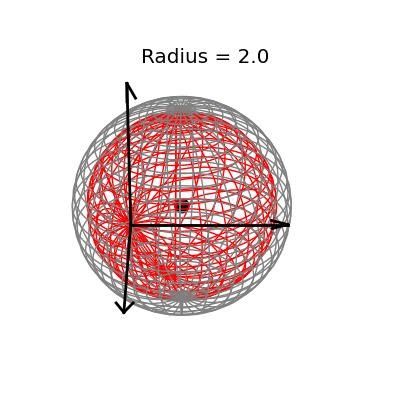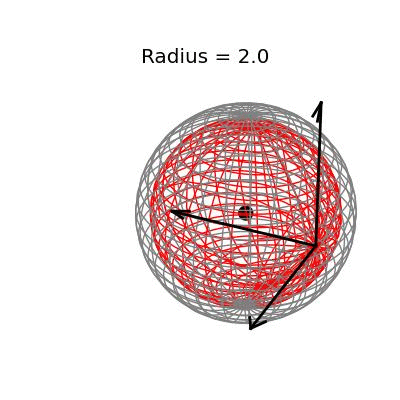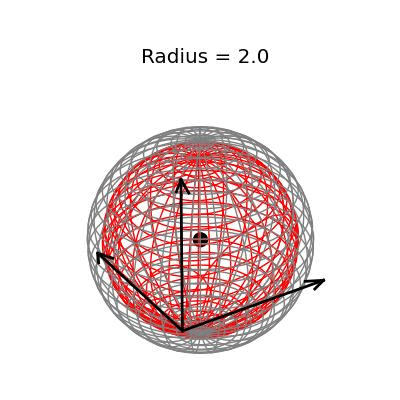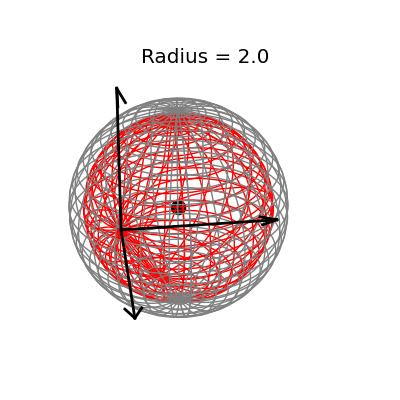
Fortunately, this phenomenon holds in dimension $p = 3$, the last dimension we can visualize! For these visualizations, I set $\sigma^2 / n = 1$, and plotted spheres of various radii around the vector $(1, 1, 1)^T$, which are the equiprobability surfaces for the distribution of the sample mean. I then applied the James-Stein estimator to the points on those spheres to see how it distorts them. In the following plots, the drawn axis have length three and the large black dot is at the point $(1, 1, 1)^T$. The grey object is the sphere centered at $(1, 1, 1)^T$, and the red object is the James-Stein estimator applied to the points on the sphere.
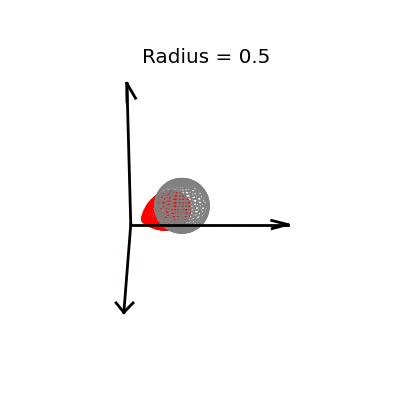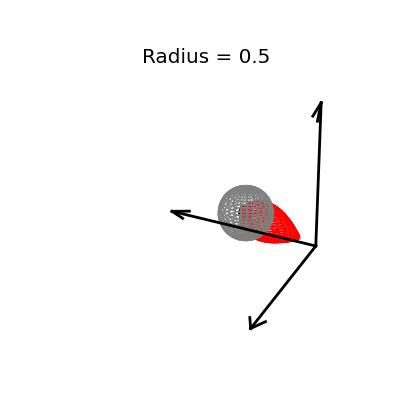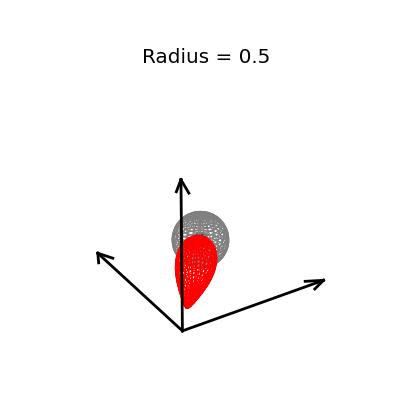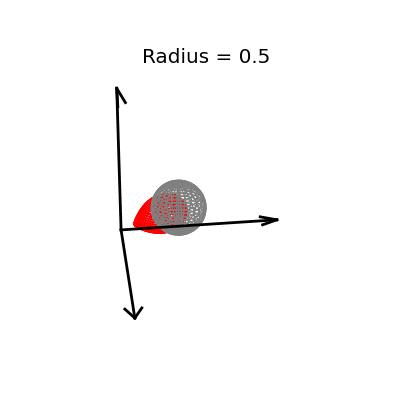
Each of these three plots shows different dynamics of the James-Stein estimator: For the smallest sphere, of radius one half, you can see that the James-Stein estimator leads to substantial bias. A three dimensional multivariate normal distribution with covariance matrix $I_3$ is not usually so close to it's mean--it's at distance 0.5 or less with probability only 3.1%. Thus, in this instance the James-Stein estimator is shrinking too aggressively, leading to bias.
The medium sized sphere, of radius one, is I think the most interesting of the plots. You can see the how the shrinking actually makes many of the points substantially closer to the point $(1, 1, 1)^T$, and you can also see how some of the points have been "overshrunk" past zero--it is because of this effect that the James-Stein estimator is itself not admissible; truncating the multiplicative factor at zero leads to a uniformly better estimator. The three dimensional multivariate normal distribution with identity covariance matrix is this close or closer to its mean 19.9% of the time.
The largest sphere, of radius two, contains the origin. Although it appears from the plot that the James-Stein estimator simply transforms this sphere into a smaller sphere inside of it, this simple story is not actually true: For example, the point $(-0.155 -0.155, -0.155)^T$, the closest point on the sphere to the origin, gets overshrunk way past the origin to the point $(2, 2, 2)^T$. This is why the transformed sphere has a few lines criss-crossing every which way, while the origin sphere has nice straight latitude and longitude lines. The three dimensional multivariate normal distribution with identity covariance matrix is this close or closer to its mean 73.9% of the time.
Thinking about the geometric picture, I think, really helps us to see why we stand to gain by shrinking: Consider a sphere somewhere which does not contain the origin. If we could shrink any point as much as we wanted, (not necessarily with James-Stein), which of the points on that sphere could we actually make closer to their center? The answer is that more than half of the sphere would get improved this way, regardless of how far away the sphere is from the origin. This is a bit of a pain to plot in three dimensions, but here's the two dimensional version: I break up the following circles into two parts: Everything within the dotted lines does worse when you shrink it towards the origin, and everything outside the dotted lines can do better if you shrink it towards the origin somewhat.
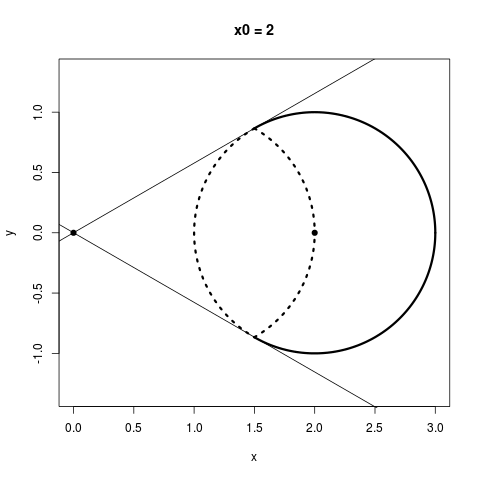
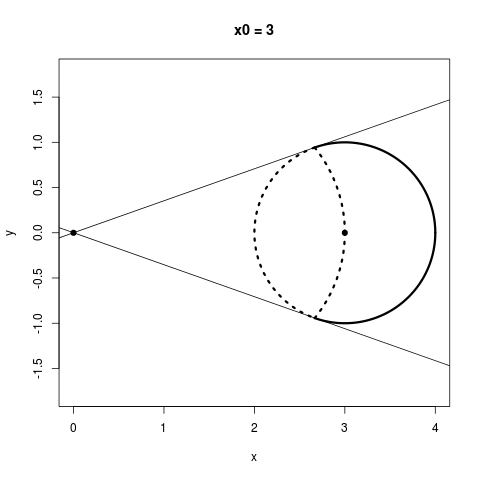
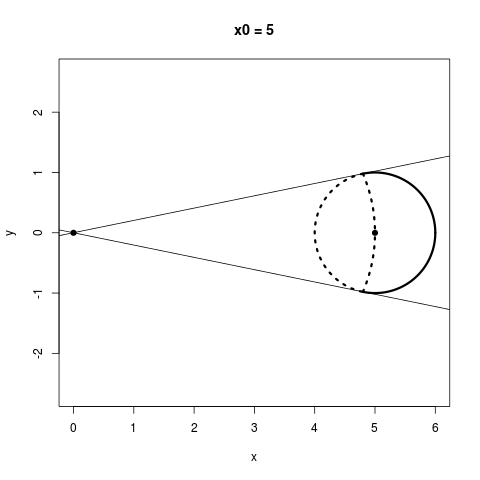
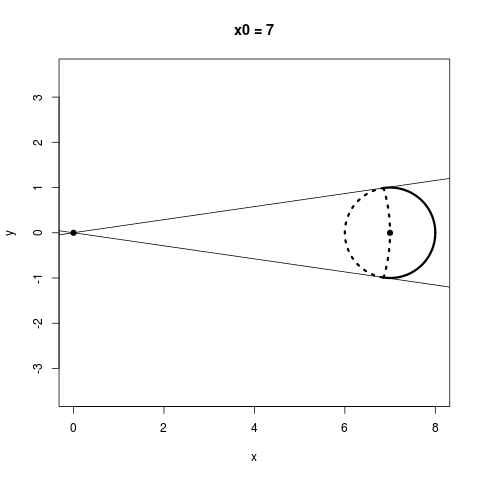
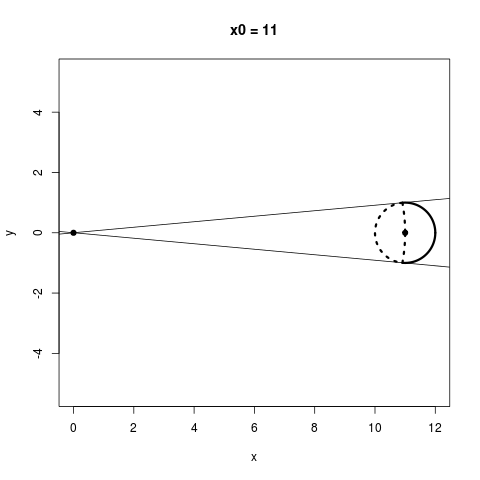
No matter how far away a sphere is from the origin, more than half of its points always have the potential to improve from shrinking. An interesting thing to notice, however, is that in the James-Stein estimator, the points you'd like to shrink the most, namely, the ones on the farther side of the circle from the origin, end up getting shrunk the least, while the points you want to shrink little or not at all end up getting shrunk the most because they are on the nearer side of the circle from the origin. This is because, for a point $X$, the James-Stein estimator moves that point by a distance proportional to $1 / \|X\|$.
The James-Stein estimator really is a magnificent idea. Although it is initially very counterintuitive, we can gain some insights into why it works by visualizing its geometry.

